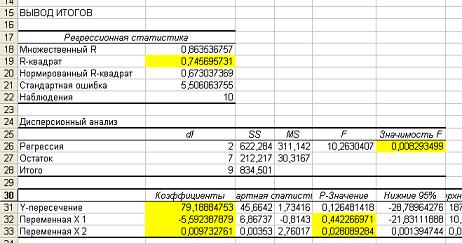
В таблице Дисперсионный анализ оценивается общее качество полученной модели: ее достоверность по уровню значимости критерия Фишера - р, который должен быть меньше, чем 0,05 (строка Регрессия, столбец Значимость F).
Значение R-квадрат описывает степень точности описания моделью процесса (вторая строка сверху в таблице Регрессионная статистика).
Далее определяем значения коэффициентов модели. Они определяютя из таблицы в столбце Коэффициенты - в строке Y-пересечение - свободный член, в строках соответствующих переменных - значения коэффициентов при этих переменных.
В столбце р-значение приводится достоверность отличия соответствующих коэффициентов от нуля.
В случае, когда р>0,05, коэффициент может считаться нулевым. Это означает, что соответствующая независимая переменная практически не влияет на зависимую переменную и коэффициент может быть убран из уравнения.

Именно поэтому в данной задаче дается такая интерпретация: Достоверность по уровню значимости критерия Фишера (Значимость F) значительно меньше 0,05, значит модель значима.
Степень точности описания моделью процесса R-квадрат равен 0,75, что говорит о высокой точности аппроксимации (модель хорошо описывает процесс).
p-значение для коэффициента х₁ больше 0,05, значит этот коэффициент может считаться нулевым.
p-значение для коэффициента х₂ меньше 0,05, значит этот коэффициент может считаться не нулевым.
Значение свободного члена (Y-пересечение) 79,19.
Отсюда уравнение для расчета выхода телят на 100 коров (y) от среднегодового потребления кормовых единиц (x₂) и среднего возраста стада (x₁) будет иметь вид y=0,0097x₂+79,19 с достоверностью R²=75%.