Задача 3 - образец решения

В результате 10-летних наблюдений за молочным стадом были получены следующие материалы, приведенные в таблице: выход телят на 100 голов (y); средний возраст стада, лет (х₁); среднегодовое потребление кормовых единиц (х₂). Построить линейное уравнение зависимости вида y=ax₁+bx₂+c и определить его достоверность R².
Наблюдаемые показатели

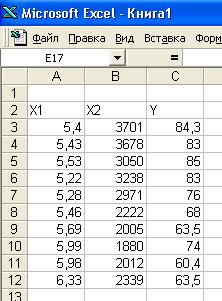
Х1	5,4	5,43	5,53	5,22	5,28	5,46	5,69	5,99	5,98	6,33
Х2	3701	3678	3050	3238	2971	2222	2005	1880	2012	2339
Y	84,3	83	85	83	76	68	63,5	74	60,4	63,5

Решение
Введем исходные данные, как на рисунке.

Для построения регрессионного уравнения необходимо активизировать «Пакет анализа» (если он установлен). Для этого в меню Сервис -> Надстройки установить флажок на «Пакет анализа».
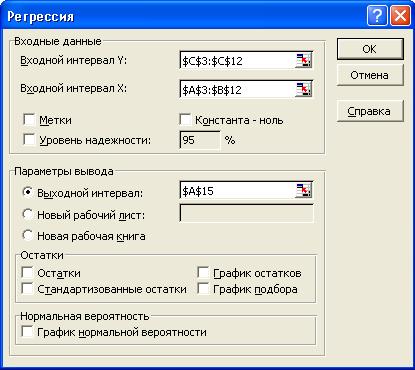
Запустим инструмент «Регрессия» (меню Сервис -> Анализ данных -> Регрессия). В открывшемся окне (см. рис.) указать: Входные данные – входной Y ввести диапазон данных Y (С3:С12 – это значения зависимой переменной Y); Входной Х ввести диапазон данных Х₁ и Х₂ (А3:В12 – это значения независимых переменных Х₁ и Х₂). В Параметрах вывода установить переключатель на Выходной интервал и указать А15. После этого нажать кнопку ОК.

Результаты выполненной работы приведены на рисунке. Дадим им интерпретацию (справка).

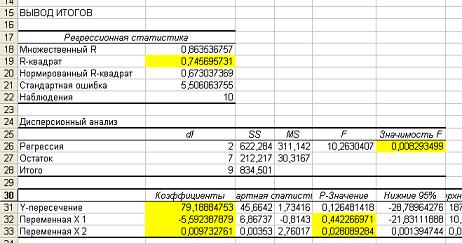
Достоверность по уровню значимости критерия Фишера (Значимость F) значительно меньше 0,05, значит модель значима.
Степень точности описания моделью процесса R-квадрат равен 0,75, что говорит о высокой точности аппроксимации (модель хорошо описывает процесс).
p-значение для коэффициента х₁ больше 0,05, значит этот коэффициент может считаться нулевым.
p-значение для коэффициента х₂ меньше 0,05, значит этот коэффициент может считаться не нулевым.
Значение свободного члена (Y-пересечение) 79,19.
Отсюда уравнение для расчета выхода телят на 100 коров (y) от среднегодового потребления кормовых единиц (x₂) и среднего возраста стада (x₁) будет иметь вид y=0,0097x₂+79,19 с достоверностью R²=75%.